Haskell Dice of Doom - Part 2

We continue our port of the Land of Lisp game “Dice of Doom” from Part 1.

In this part, we:

Display the game tree graphically.
Fix a bug.
Develop the AI player.

Displaying the Game Tree

As we dive into developing the AI for the game, we’ll need more interesting game trees to play around with. The game tree in Part 1 wasn’t particularly good from a game play point of view - B always wins, and reinforcements never come up.

If we want to look at different trees it would be helpful if we could display them a bit better. Neither the Lisp nor the Haskell version of the game tree output is user-friendly.

A very simple initial approach is to use the drawTree function in Data.Tree:

ghci> :t drawTree
drawTree :: Tree String -> String
ghci> let tree = Node "A" [Node "B" [], Node "C" [Node "D" [], Node "E" []]]
ghci> putStrLn $ drawTree $ tree
A
|
+- B
|
`- C
   |
   +- D
   |
   `- E

The problem is that this only works with string trees. We need to convert our Tree GameState to a Tree String. To do this we use the fact that Data.Tree is a functor. We can use fmap on the tree to produce another tree with exactly the same tree structure but with the nodes transformed in some way. Our transformation function must convert from a GameState value to a String. We have such as function: show. Let’s change the GameState data type to have a custom show method:

data GameState = GameState {
                    currentPlayer :: Player,
                    moveMade :: Move,
                    currentBoard :: Board
                 }

instance Show GameState where
    show g = "Player: " ++ show (currentPlayer g) ++
             " Board: " ++ show (cells $ currentBoard g) ++ 
             " Move: " ++ show (moveMade g) ++
             " Reinforcements : " ++ show (conqueredDice $ currentBoard g) ++
             " Winners: " ++ show (winners $ currentBoard g)

Note that the winners means the current node’s winners and not the overall game winner.

Now to display the tree we use fmap:

ghci> let tree = gameTree test2x2Board (Player 0) Pass True
ghci> putStrLn $ drawTree $ fmap show tree
Player: a Board: [b-2,b-2,a-2,b-1] Move: Pass Reinforcements : 0 Winners: [b]
|
`- Player: a Board: [b-2,b-2,a-1,a-1] Move: Attack 2 3 Reinforcements : 1 Winners: [a,b]
   |
   `- Player: b Board: [b-2,b-2,a-1,a-1] Move: Pass Reinforcements : 0 Winners: [a,b]
      |
...

We can put this into a drawGameTree function in several ways:

drawGameTree :: Tree GameState -> IO ()
drawGameTree tree = putStrLn $ drawTree $ fmap show tree

Or, using function composition:

drawGameTree :: Tree GameState -> IO ()
drawGameTree tree = putStrLn . drawTree . fmap show $ tree

Or, using point-free notation:

drawGameTree :: Tree GameState -> IO ()
drawGameTree = putStrLn . drawTree . fmap show

Code in DiceOfDoom-f.hs.

Using Graphviz To Display The Game Tree

Displaying the game tree in ASCII is nice, but with a bit more work we can do a lot better. In Chapter 7 of Land of Lisp, Graphviz is used to display a graph of the role-playing game. We can do something similar here.

A Graphviz graph is simply:

A list of nodes and what they contain.
What connects the nodes.

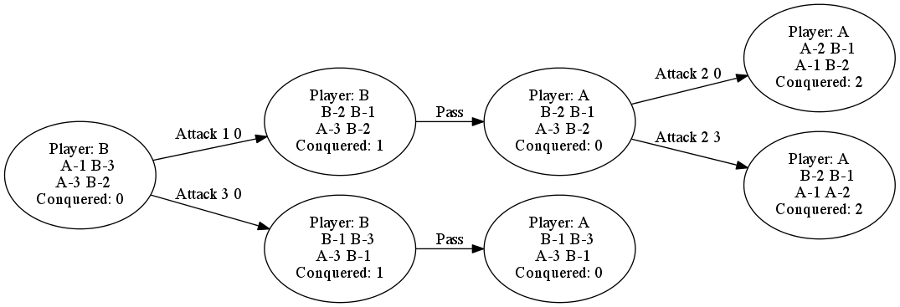
Here’s a simple example of the sort of output we would like:

digraph G {
    rankdir=LR;

    "0" [color=black;label="Player: B\n    A-1 B-3\n  A-3 B-2\nConquered: 0";]
    "1" [color=black;label="Player: B\n    B-2 B-1\n  A-3 B-2\nConquered: 1";]
    "2" [color=black;label="Player: A\n    B-2 B-1\n  A-3 B-2\nConquered: 0";]
    "3" [color=black;label="Player: A\n    A-2 B-1\n  A-1 B-2\nConquered: 2";]
    "4" [color=black;label="Player: A\n    B-2 B-1\n  A-1 A-2\nConquered: 2";]
    "5" [color=black;label="Player: B\n    B-1 B-3\n  A-3 B-1\nConquered: 1";]
    "6" [color=black;label="Player: A\n    B-1 B-3\n  A-3 B-1\nConquered: 0";]

    "0" -> "1" [label="Attack 1 0";];
    "0" -> "5" [label="Attack 3 0";];
    "5" -> "6" [label="Pass";];
    "1" -> "2" [label="Pass";];
    "2" -> "3" [label="Attack 2 0";];
    "2" -> "4" [label="Attack 2 3";];
}

Here the “0”, “1” etc. are just node numbers - we don’t care what they really are, so long as they uniquely identify a node.

Running this through Graphviz and selecting PNG output:

dot -Tpng testgraph.dot -o testgraph.png

we get:

testgraph

Numbering a Tree

In order to do this we’ll need to uniquely identify each node in the tree. We could try to do this while constructing the game tree, but it’s probably easier to come up with some transformation function that replaces each node with a pair of the original node and a unique integer:

numberTree :: Tree a -> Tree (a, Int)

This is the sort of thing that’s really trivial to do in a non-functional language: set a counter to zero, traverse the tree, pair the node with the counter value, increment the counter and recurse. In pure functional languages like Haskell, it’s a little bit more involved (but not much more), because we can’t just increment some counter willy-nilly. Haskell provides us with mechanisms for managing such state. In particular, the State Monad.

Just beware: you might think that numberTree could be implemented using fmap and some appropriate function, in a similar way that we converted the tree to a tree of strings. This won’t work. The function used in fmap gets the contents of the node and not the node itself. The function doesn’t even know that it’s dealing with a tree. You might also think that you could just re-build the tree using recursion. This also won’t work. There’s no getting away from it - we need to use something stateful.

Tree numbering is used as an example of using the State Monad in the Hackage page for Control.Monad.State.Lazy. The example is taken from Simon Thompson’s book Haskell - The Craft of Functional Programming, chapter 18. The example there needs to keep track of using the same number if the node contents are the same, which we don’t have to do.

There’s also an example in Graham Hutton’s paper Programming with Effects.

Both Hutton’s and Thompson’s examples use a hand-crafted version of the State Monad instead of the one in Control.Monad.State, which is what we’ll use now.

With the help of Kim-Ee Yeoh from the Haskell Beginners mailing list, we have the following implementation:

numberTree :: Tree a -> Tree (a, Int)
numberTree t = evalState (numTree t) 0
   where
        numTree :: Tree a -> State Int (Tree (a, Int))
        numTree (Node root children) =  do 
            num <- nextNumber
            newChildren <- mapM numTree children 
            return $ Node (root, num) newChildren
            where 
                nextNumber :: State Int Int
                nextNumber = do 
                    n <- get
                    put (n + 1)
                    return n

A bit of explanation: the numberTree function evaluates the state produced in the inner function numTree, which executes in the State Monad. It uses another function, nextNumber to manage a counter. The important thing here is that when recusing using state monads, you need to use mapM to map the stateful function numTree over the list of child nodes.

Testing this we have:

ghci> :l DiceOfDoom-f.hs
ghci> let testTree = Node "A" [Node "B" [], Node "C" [Node "D" [], Node "E" []]]
ghci> numberTree testTree
Node {
    rootLabel = ("A",0), 
    subForest = [
        Node {
            rootLabel = ("B",1), 
            subForest = []
        },
        Node {
            rootLabel = ("C",2), 
            subForest = [
                Node {
                    rootLabel = ("D",3), 
                    subForest = []
                },
                Node {rootLabel = ("E",4), subForest = []} ]}]}

Generating Graphiz Output

With this in place, we can start on our Graphviz output.

Note: There is a package on Hackage, graphviz, for producting Graphviz output. There’s also the Diagrams package. However, for this example we’ll just format a bunch of strings as the output.

The function to get the list of nodes with their contents is showGameGraphNodes. Note that it uses Text.Printf to do some formatting.

showGameGraphNodes :: Tree (GameState, Int) -> String
showGameGraphNodes (Node (gstate, number) children) = 
    concat $ 
        (nodeStr ++ " " ++ labelStr) :
        [showGameGraphNodes c | c <- children] 
    where
        nodeStr = printf "\"%d\"" number :: String
        board = currentBoard gstate
        boardStr = showBoard board
        playerStr = printf "Player: %s" (show $ currentPlayer gstate) :: String
        diceStr = printf "Conquered: %s" (show $ conqueredDice board) :: String
        winnersColour = if null children
                        then case winners board of 
                                [Player 0] -> "lightpink;style=filled"
                                [Player 1] -> "lightblue;style=filled"
                                _          -> "lightgreen;style=filled"
                        else "black"
        labelStr = printf "[color=%s;label=\"%s\\n%s%s\";]\n" 
                        winnersColour playerStr boardStr diceStr :: String

We colour the leaf nodes with the winner - blue for B, pink for A and green for a tie.

Getting the relationship between the nodes is similar:

showGameGraphTree :: Tree (GameState, Int) -> String
showGameGraphTree (Node (_, number) children) = 
    concat $ [
                printf "\"%d\" -> \"%d\" [label=\"%s\";];\n" 
                        number child_number (show $ moveMade child) :: String
                | (Node (child, child_number) _) <- children] ++
             [showGameGraphTree c | c <- children]

Putting this all together we have:

drawGraphvizTree :: Tree GameState -> IO ()
drawGraphvizTree = putStrLn . showGraphvizTree

showGraphvizTree :: Tree GameState -> String
showGraphvizTree tree = "digraph G {\n" ++
    "rankdir=LR;\n" ++
    showGameGraphNodes (numberTree tree) ++
    showGameGraphTree (numberTree tree) ++ 
    "}"

Automating The Generation of SVG Files

We can test this out in GHCI by running the function and copy and pasting the Graphviz output into a file, but that’s tedious. Let’s automate the generation of the graph output by writing a function that runs the Graphviz dot command for us. The function creates a process for the dot command and ties the stdin of that proceess to the Graphviz string representation:

makeGraphvizFile :: String -> String -> IO ()    
makeGraphvizFile graphvizData fileName = do
    (Just hIn, _, _, jHandle) <-
        createProcess (proc "dot" ["-Tsvg", "-o", fileName ++ ".svg"])
           { cwd = Just "."
           , std_in = CreatePipe
           }
    hPutStr hIn graphvizData 
    hClose hIn
    exitCode <- waitForProcess jHandle
    case exitCode of
        ExitSuccess -> putStr ""
        _           -> putStrLn "DOT command failed"

Let’s test this out on the 2x2 board used in part 1:

ghci> :l DiceOfDoom-f.hs
ghci> let gt = showGraphvizTree $ gameTree test2x2Board (Player 0) Pass True
ghci> makeGraphvizFile gt "test2x2board"

You should see this when you open the SVG file:

Fixing A Bug

The reason I spent a good while getting a nice graphical display of the game tree is because I discovered a bug in the Haskell code to do with how conquered dice are gathered. I only found this when looking at a more complicated game tree (see below).

The bug is in the makeAMove code:

    | canAttack board src dest = 
        board {
            cells = [afterAttack (pos, c) | (pos, c) <- cellPositions board],
            conqueredDice = destDice
        }

We should be adding the dice conquered in the current move to the board’s tally of conquered dice:

    | canAttack board src dest = 
        board {
            cells = [afterAttack (pos, c) | (pos, c) <- cellPositions board],
            conqueredDice = conqueredDice board + destDice
        }

In the game tree in Part 1 the reinforcement scenario never arose.

That’s fixed in DiceOfDoom-f.hs.

Creating an AI Player

For a two-player game, we use the Minimax algorithm to drive the AI player’s decisions.

Let’s consider a more complex 2x2 game where all three possible outcomes can arise:

test2x2BoardC :: Board
test2x2BoardC = Board {
    size = 2,
    maxDice = 3,
    numPlayers = 2,
    cells = [
          Cell {player = Player 0, dice = 3}
        , Cell {player = Player 0, dice = 3}
        , Cell {player = Player 1, dice = 2}
        , Cell {player = Player 1, dice = 3}],
    conqueredDice = 0
}

The board is much more evenly balanced. If we look at the game tree where player A starts, we see that all three winning combinations are possible for both players:

(Right-click to open in a new tab to see a full scale SVG).

The Minimax Algorithm

For 2-player games, the Minimax Algorithm involves computing a rating for the position of a player in the tree. We move along the tree as far as we can go, until we reach a point where there are no more moves. At that point, we calculate a score based on whether the current player is in the list of winners for that board position. If the current player is the only one in the list of winners, the score is 1. If it’s a tie, the score is 0.5, and if the player isn’t on the list, the score is 0.

ratePosition :: Tree GameState -> Player -> Double
ratePosition tree@(Node root children) nodePlayer  
    | null children =
        -- Can't go any further - rate the current board
        if nodePlayer `elem` nodeWinners
            then 1.0 / fromIntegral (length nodeWinners)
            else 0.0
    | otherwise = 
        -- Keep going
        if nodePlayer == currentPlayer root
            then maximum $ childRatings tree nodePlayer
            else minimum $ childRatings tree nodePlayer
    where
        nodeWinners :: [Player]
        nodeWinners = winners $ currentBoard root
        
childRatings :: Tree GameState -> Player -> [Double]
childRatings (Node _ children) nodePlayer = [ratePosition c nodePlayer | c <- children]

The AI code is similar to the playVsHuman equivalent:

playVsComputer :: Tree GameState -> IO ()
playVsComputer tree@(Node root children) = do
    printGameState tree
    if not (null children)
        then 
            playVsComputer =<< 
                if currentPlayer root == Player 0 -- by convention, the human
                then
                    handleHuman tree
                else
                    handleComputer tree
        else 
            announceWinner $ currentBoard root 

handleComputer :: Tree GameState -> IO (Tree GameState)
handleComputer tree@(Node root children) = do
    let moveChosen = Map.lookup childPosChosen mapOfMoves 
    case moveChosen of
        Just m -> do
            putStrLn $ "  ---> " ++ show m
            return $ children !! (childPosChosen  - 1)
        Nothing -> do
            putStrLn $ "This should never happen: " ++ show childPosChosen
            handleComputer tree
    where 
        ratings :: [Double]
        ratings = childRatings tree (currentPlayer root)
        maxPos :: Ord a => [a] -> Int
        maxPos xs = snd $ maximum $ zip xs [1..]
        childPosChosen :: Int
        childPosChosen = maxPos ratings
        allowedMoves :: [(Int, Move)]
        allowedMoves = zip [1..] [moveMade c | (Node c _) <- children]
        mapOfMoves :: Map.Map Int Move
        mapOfMoves = Map.fromList allowedMoves

We can now play against the AI:

ghci> playVsComputer $ gameTree test2x2BoardC (Player 0) Pass True
Current player: A
    A-3 A-3
  B-2 B-3
choose your move:
1: Attack 0 2
1
Current player: A
    A-1 A-3
  A-2 B-3
choose your move:
1: Pass
1
Current player: B
    A-2 A-3
  A-2 B-3
  ---> Attack 3 2
Current player: B
    A-2 A-3
  B-2 B-1
  ---> Pass
Current player: A
    A-2 A-3
  B-3 B-1
choose your move:
1: Attack 0 3
2: Attack 1 3
1
Current player: A
    A-1 A-3
  B-3 A-1
choose your move:
1: Pass
1
Current player: B
    A-1 A-3
  B-3 A-1
  ---> Attack 2 3
Current player: B
    A-1 A-3
  B-1 B-2
  ---> Pass
Current player: A
    A-1 A-3
  B-1 B-2
choose your move:
1: Attack 1 3
1
Current player: A
    A-1 A-1
  B-1 A-2
choose your move:
1: Attack 3 2
2: Pass
1
Current player: A
    A-1 A-1
  A-1 A-1
choose your move:
1: Pass
1
Current player: B
    A-2 A-2
  A-1 A-1
The winner is [A]

Code is DiceOfDoom-f.hs.

Making Play the Same as the Lisp Version

NOTE If you compare the play against the Lisp version, you will see some differences. I’d like to make the two versions play the same, because it’s easier for testing.

The first difference is the way the node is chosen among those with the same rating. In Haskell we have the following to find the position of child with the maximum rating:

maxPos :: Ord a => [a] -> Int
maxPos xs = snd $ maximum $ zip xs [1..]

Trying this out on a list of 1 0 1 0 1 0 we have:

ghci> maxPos [1, 0, 1, 0, 1, 0]
5

In Lisp, we have:

(position (apply #'max ratings) ratings)

This gives:

[1]> (defvar ratings '(1 0 1 0 1 0))
RATINGS
[2]> (position (apply #'max ratings) ratings)
0

The Haskell version gives the last maximum found, whereas the Lisp version gives the first.

Let’s fix this using elemIndex to find the first matching item.

maxPos :: Ord a => [a] -> Int
maxPos xs = case elemIndex (maximum xs) xs of
    Just x -> x + 1
    _      -> 0

We need the “+ 1” because, for user display purposes, we map the child movements to 1, 2, 3 … but elemIndex returns a 0-based index. Note that we should never get to the second part of the case statement, so putting a “0” in there seems safe.

The next difference is that the Lisp version always presents the “Pass” option first. In the gameTree function we have:

| m <- possibleMoves ++ addPassingMove]

We can change this to:

| m <- addPassingMove ++ possibleMoves]

While we’re making changes, I don’t like hard-coding player A as the human, so let’s parameterise it:

playVsComputer :: Player -> Tree GameState -> IO ()
playVsComputer computerPlayer -> tree@(Node root children) = do
    printGameState tree
    if not (null children)
        then 
            playVsComputer computerPlayer =<< 
                if currentPlayer root == computerPlayer 
                then
                    handleComputer tree
                else
                    handleHuman tree
        else 
            announceWinner $ currentBoard root

Finally, there’s duplicate code used in handleHuman and handleComputer which I’ve factored that out.

Code in DiceOfDoom-g.hs.

Computer vs Computer

There’s nothing stopping us playing the AI against itself.

playComputerVsComputer :: Tree GameState -> IO ()
playComputerVsComputer tree@(Node root children) = do
    printGameState tree
    if not (null children)
        then 
            playComputerVsComputer =<< handleComputer tree
        else 
            announceWinner $ currentBoard root

ghci> let gt = gameTree test2x2BoardC (Player 0) Pass True
ghci> playComputerVsComputer (Player 0) gt
Current player: A
    A-3 A-3
  B-2 B-3
  ---> Attack 0 2
Current player: A
    A-1 A-3
  A-2 B-3
  ---> Pass
Current player: B
    A-2 A-3
  A-2 B-3
  ---> Attack 3 0
Current player: B
    B-2 A-3
  A-2 B-1
  ---> Pass
Current player: A
    B-3 A-3
  A-2 B-1
  ---> Attack 2 3
Current player: A
    B-3 A-3
  A-1 A-1
  ---> Pass
Current player: B
    B-3 A-3
  A-1 A-1
  ---> Attack 0 2
Current player: B
    B-1 A-3
  B-2 A-1
  ---> Pass
Current player: A
    B-1 A-3
  B-2 A-1
  ---> Attack 1 0
Current player: A
    A-2 A-1
  B-2 A-1
  ---> Pass
Current player: B
    A-2 A-1
  B-2 A-1
  ---> Attack 2 3
Current player: B
    A-2 A-1
  B-1 B-1
  ---> Pass
Current player: A
    A-2 A-1
  B-1 B-1
  ---> Attack 0 2
Current player: A
    A-1 A-1
  A-1 B-1
  ---> Pass
Current player: B
    A-1 A-1
  A-1 B-1
The winner is [A]

That’s it for Part 2. We can now play 2x2 games against an AI opponent. In Part 3, we’ll take a close look at performance, which will allow us to play 3x3 or larger boards.