Conrad Barski’s Land of Lisp develops a simple board game from chapter 15 onwards, as an example of using functional-style programming in Common Lisp. The game, Dice of Doom, uses a hexagonally-tiled board where two or more players occupy various cells on the board and can attack each other subject to some rules.
In this series we’ll rewrite the game using Haskell.
The source code for this can be found on Github: Dice of Doom
The Original Lisp Game
The source code for the Lisp version can be found here.
Alternatively use dice_of_doom_v1.lisp that accompanies this source.
Download this file.
To run it you’ll need a working CLisp or SBCL environment. We’ll use CLisp to test the run:
$ clisp
...
[1]> (load "dice_of_doom_v1.lisp")
;; Loading file dice_of_doom_v1.lisp ...
;; Loaded file dice_of_doom_v1.lisp
T
[2]> (play-vs-human (game-tree (gen-board) 0 0 t))
current-player = a
b-2 a-1 a-1
a-2 b-2 a-3
b-3 b-1 b-1
choose your move:
1. 3 -> 7
2. 5 -> 8
3. 5 -> 4(Note: to quit during play, press CTRL-C and then (quit) at the CLisp prompt.)
The above 3x3 board looks like this:
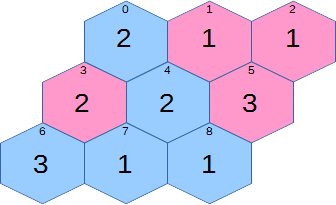
The rules of the game are as follows:
- Two players (named A and B) occupy spaces on a hexagonal grid. Each hexagon in the grid will have some six-sided dice on it, owned by the occupant.
- During a turn, a player can perform any number of moves, but must perform at least one move. If the player cannot move, the game ends.
- A move consists of attacking a neighboring hexagon owned by the opponent. The player must have more dice in her hexagon than the neighboring hexagon in order to attack. For now, all attacks will automatically lead to a win. In future variants, we’ll actually roll the dice for a battle. But for now, the player with more dice just wins automatically.
- After winning a battle, the losing player’s dice are removed from the board, and all but one of the winning player’s dice are moved onto the newly won hexagon.
- After a player is finished making her moves, reinforcements are added to that player’s dice armies. Reinforcements to the player’s occupied hexagons are added one die at a time, starting from the upper-left corner, moving across and down. The maximum number of dice added as reinforcements is one less than the player took from the opponent in her completed turn.
- When a player can no longer take her turn, the game has ended. The player who occupies the most hexagons at this point is the winner. (A tie is also possible.)
Play a few rounds to get used to the mechanics.
NOTE: If you’re playing around with this, don’t set the board size to anything bigger than 3. The initial version of the Lisp game is very inefficient and it will hang for a long time.
Setting up the Data Types in Haskell
The Lisp implementation uses integer values to represent the state of the board:
[2]> (gen-board)
#((1 2) (0 1) (0 1) (0 2) (1 2) (0 3) (1 3) (1 1) (1 1))An array (not a list) of tuples is used, mainly for performance reasons. This is often done in Haskell for the same reasons - constant-time access to a resource.
The first item in the tuple is the player (0 or 1) owning the cell, and the second item is the number of dice (1, 2 or 3) in that cell.
We could do something similar in Haskell:
type Board = [(Int, Int)]But this is Haskell, and we should use the type system to our advantage:
data Player = Player Int
deriving (Show)
data Cell = Cell {
player :: Player,
dice :: Int
}
deriving (Show)
data Board = Board {
size :: Int,
maxDice :: Int,
numPlayers :: Int,
cells :: [Cell],
conqueredDice :: Int
}
deriving (Show)
test2x2Board :: Board
test2x2Board = Board {
size = 2,
maxDice = 3,
numPlayers = 2,
cells = [
Cell {player = Player 1, dice = 2}
, Cell {player = Player 1, dice = 2}
, Cell {player = Player 0, dice = 2}
, Cell {player = Player 1, dice = 1}],
conqueredDice = 0
}
test3x3Board :: Board
test3x3Board = Board {
size = 3,
maxDice = 3,
numPlayers = 2,
cells = [
Cell {player = Player 0, dice = 1}
, Cell {player = Player 1, dice = 2}
, Cell {player = Player 0, dice = 1}
, Cell {player = Player 1, dice = 1}
, Cell {player = Player 1, dice = 2}
, Cell {player = Player 0, dice = 1}
, Cell {player = Player 0, dice = 1}
, Cell {player = Player 0, dice = 1}
, Cell {player = Player 0, dice = 3}],
conqueredDice = 0
}Note that I’m putting more state into the board than the Lisp version - including the board dimensions and the number of dice conquered in an attacking move.
Generating a Random Board
The Lisp code in the book marks out the sections of the code that have a “clean, functional” style vs. those that have a “dirty, imperative” style.
The Lisp code to generate a randomly populated board is not functional, and has the “dirty, imperative” icon:

(defun board-list ()
(loop for n below *board-hexnum*
collect (list (random *num-players*)
(1+ (random *max-dice*)))))Haskell allows us to mark the code directly as “dirty”, “imperative” or “unsafe”. We do this using the IO monad.
import System.Random (newStdGen, randomRs)
genBoard :: Int -> Int -> Int -> IO Board
genBoard boardSize nplayers ndice = do
diceGen <- newStdGen
playerGen <- newStdGen
let players = map Player $ take numCells $ randomRs (0, nplayers - 1) playerGen
let dice_values = take numCells $ randomRs (1, ndice) diceGen
return Board {
size = boardSize,
maxDice = ndice,
numPlayers = nplayers,
cells = [Cell {player = p, dice = n} | (p, n) <- zip players dice_values],
conqueredDice = 0
}
where
numCells = boardSize * boardSizeCode is in DiceOfDoom-a.hs
Note: unlike the original code, the board size, number of players and number of dice are passsed in as parameters.
We can test this in the repl:
ghci> :l dice-of-doom.hs
ghci> board <- genBoard 3 2 3
ghci> board
Board {
size = 3,
maxDice = 3,
numPlayers = 2,
cells = [
Cell {player = Player 0, dice = 1},
Cell {player = Player 0, dice = 3},
Cell {player = Player 0, dice = 3},
Cell {player = Player 1, dice = 1},
Cell {player = Player 0, dice = 1},
Cell {player = Player 1, dice = 3},
Cell {player = Player 1, dice = 3},
Cell {player = Player 1, dice = 3},
Cell {player = Player 1, dice = 2}
],
conqueredDice = 0
}Drawing The Board
The data types given so far use the default implementation of the Show typeclass.
We’ll change that now to represent the board in the same way as the Lisp code.
Drawing the board is another “unsafe” function, but I’ll split it into two functions: one does the IO, the other generates a string representation of the board.
First we’ll remove the default implementation of the Show typeclass for Player and Cell
and replace them with a custom version:
import Data.List (chr, ord)
data Player = Player Int
instance Show Player where
show (Player i) = [chr (i + ord 'a')]
data Cell = Cell {
player :: Player,
dice :: Int
}
instance Show Cell where
show c = show (player c) ++ "-" ++ show (dice c)As in the Lisp version, player 0 is denoted by ‘a’, player 1 by ‘b’ etc.
This now gives us:
ghci> test3x3board
Board {
size = 3,
maxDice = 3,
numPlayers = 2,
cells = [a-1,b-2,a-1,b-1,b-2,a-1,a-1,a-1,a-3],
conqueredDice = 0
}To get the exact same as the Lisp program output, we define showBoard for the string
representation and drawBoard as the bit that does IO:
drawBoard :: Board -> IO ()
drawBoard b = putStrLn $ showBoard b
showBoard :: Board -> String
showBoard b = concatMap showRow $ zip rowNumbers rows
where
showRow (rowNo, rowCells) = indent rowNo ++ showCells rowCells
indent lineno = concat $ replicate lineno " "
showCells cs = unwords (map show cs) ++ "\n"
boardSize = size b
rowNumbers = [boardSize, boardSize -1 .. 1]
rows = chunksOf boardSize (cells b)We break down the list of cells into rows, number the rows (starting at the highest number and working down to 1), zip these together to form a tuple of (row number, cells in row), then indent depending on the row number (highest numbered rows are indented more) and concatentate the cells on each row together.
Testing this we have:
ghci> drawBoard test3x3board
a-1 b-2 a-1
b-1 b-2 a-1
a-1 a-1 a-3Code is in DiceOfDoom-b.hs
Generating a Game Tree
A game tree is a tree of all possible moves from an intial board configuration.
As an example, consider the example game on page 321. I’ve added the 2x2 board configuration used on that page as a new parameter in the Lisp code:
(defparameter *test-board* #((1 2) (1 2) (0 2) (1 1)))(Note: this is the same as the test2x2Board in the Haskell source.
You can play out this game in CLisp:
[1]> (load "dice_of_doom_v1.lisp")
;; Loading file dice_of_doom_v1.lisp ...
;; Loaded file dice_of_doom_v1.lisp
T
[2]> (play-vs-human (game-tree *test-board* 0 0 t))
current player = a
b-2 b-2
a-2 b-1
choose your move:
1. 2 -> 3We’re interested in the game tree, as produced by the game-tree function. Let’s take
a look at what it produces:
[1]> (load "dice_of_doom_v1.lisp")
;; Loading file dice_of_doom_v1.lisp ...
;; Loaded file dice_of_doom_v1.lisp
T
[2]> (game-tree *test-board* 0 0 t))
(0 #((1 2) (1 2) (0 2) (1 1))
(((2 3)
(0 #((1 2) (1 2) (0 1) (0 1))
((NIL
(1 #((1 2) (1 2) (0 1) (0 1))
(((0 2)
(1 #((1 1) (1 2) (1 1) (0 1))
((NIL (0 #((1 1) (1 2) (1 1) (0 1)) NIL))
((1 3) (1 #((1 1) (1 1) (1 1) (1 1)) ((NIL (0 #((1 2) (1 1) (1 1) (1 1)) NIL))))))))
((0 3) (1 #((1 1) (1 2) (0 1) (1 1)) ((NIL (0 #((1 1) (1 2) (0 1) (1 1)) NIL)))))
((1 3)
(1 #((1 2) (1 1) (0 1) (1 1))
((NIL (0 #((1 2) (1 1) (0 1) (1 1)) NIL))
((0 2)
(1 #((1 1) (1 1) (1 1) (1 1)) ((NIL (0 #((1 2) (1 1) (1 1) (1 1)) NIL))))))))))))))))
... Ignore the errors and just look at the output. Whoa!
Each node in the game tree contains the current player (0 or 1), the current board state and a list of possible moves. Each move leads to another node on the tree.
The above can be summarised as follows, where we show players A and B:
A #((1 2) (1 2) (0 2) (1 1))
| A Moves 2 -> 3
+----> A #((1 2) (1 2) (0 1) (0 1))
| No A Moves Possible - B's Turn
+---> B #((1 2) (1 2) (0 1) (0 1))
| B Moves 0 -> 2
+-------> B #((1 1) (1 2) (1 1) (0 1))
| | B Ends - A's Turn
| +---> A #((1 1) (1 2) (1 1) (0 1))
| | No A Moves Possible - GAME ENDS - B wins
| | B Moves 1 -> 3
| +---> B #((1 1) (1 1) (1 1) (1 1))
| | No B Moves Possible - A's Turn
| +---> A #((1 2) (1 1) (1 1) (1 1))
| No A Moves Possible - GAME ENDS - B wins
| B Moves 0 -> 3
+-------> B #((1 1) (1 2) (0 1) (1 1))
| | No B Moves Possible
| +---> A #((1 1) (1 2) (0 1) (1 1))
| No A Moves Possible - GAME ENDS - B wins
| B Moves 1 -> 3
+-------> B #((1 2) (1 1) (0 1) (1 1))
| B Ends - A's Turn
+---> A #((1 2) (1 1) (0 1) (1 1))
| No A Moves Possible - GAME ENDS - B wins
| B Moves 0 -> 2
+---> B #((1 1) (1 1) (1 1) (1 1))
| No B Moves Possible - A's Turn
+---> A #((1 2) (1 1) (1 1) (1 1))
No A Moves Possible - GAME ENDS - B winsIt’s better to see it in a diagram:
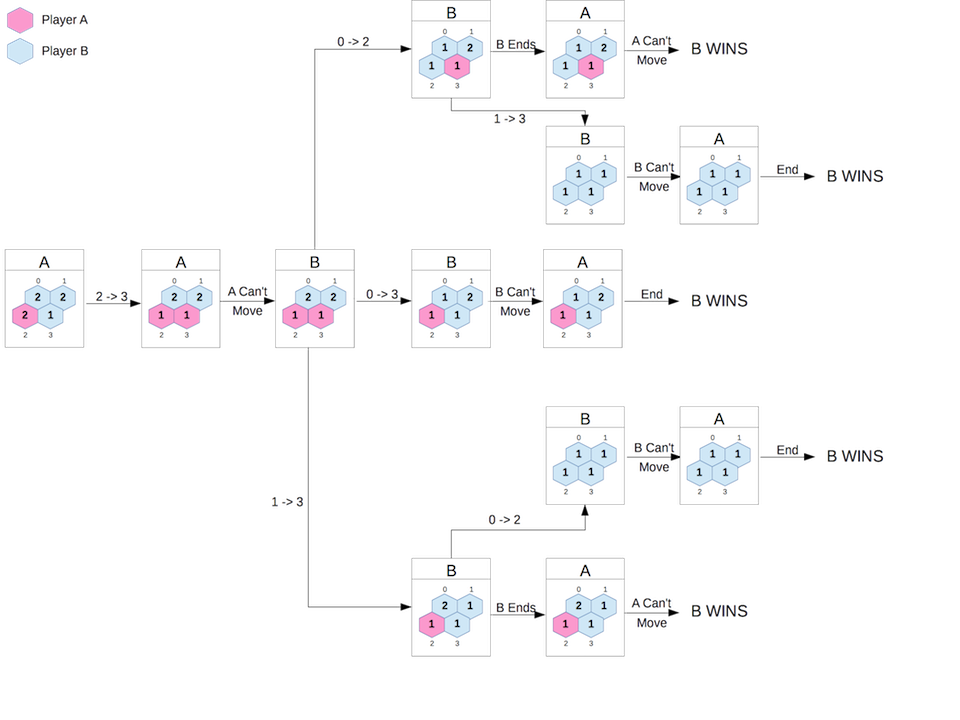
Compare this with the game tree for the same board but with B playing first:
[2]> (game-tree *test-board* 1 0 t))
(1 #((1 2) (1 2) (0 2) (1 1)) NIL)If B plays first, there are no moves possible and the game ends with B the winner.
The code do to this is split over a few functions:
- game-tree
- add-passing-move
- attacking-moves
The last two functions recurse back to the first.
Calculating Attacking Moves
Let’s look at the attacking-moves function. Given a board and a player, finding out the
list of attacking moves involves finding all the cells for that player, and for each
cell finding the list of attacking moves to the opposition’s cells that are in the
neighbourhood of the player.
The neighbours of a cell can be determined as follows:
neighbours :: Int -> Int -> [Int]
neighbours board_size pos =
[p | p <- possibleNeighbours, p >= 0 && p < (board_size * board_size)]
where
up = pos - board_size
down = pos + board_size
possibleNeighbours = [up, down]
++ (if pos `mod` board_size == 0
then []
else [up - 1, pos - 1])
++ (if (pos + 1) `mod` board_size == 0
then []
else [pos + 1, down + 1])Trying this out we have:
ghci> :l DiceOfDoom-c.hs
ghci> neighbours 3 4
[1,7,0,3,5,8]
ghci> neighbours 3 0
[3,1,4]Note that the Lisp code deals with positions of cells in the array. We’ll use that for the moment as well, but might change it later.
It’s useful to map the positions of cells with the actual cells. From that we can find the cell positions for a player:
-- Get a list of board positions and cells
cellPositions :: Board -> [(Int, Cell)]
cellPositions b = zip [0..] (cells b)
-- Find all a player's cells on a board
playerPositions :: Board -> Player -> [(Int, Cell)]
playerPositions b p = filter (\(_, c) -> player c == p) (cellPositions b)We’ll need a function to see if one cell can attack another:
-- Using cells
canCellAttack :: Cell -> Cell -> Bool
canCellAttack cell1 cell2 = player cell1 /= player cell2 && dice cell1 > dice cell2
-- Using a board and cell positions
canAttack :: Board -> Int -> Int -> Bool
canAttack b pos1 pos2 = canCellAttack cell1 cell2
where
cell1 = cells b !! pos1
cell2 = cells b !! pos2Putting this altogether, we have a function to get all the possible attack moves for a player on a particular board:
attackMoves :: Board -> Player -> [(Int, Int)]
attackMoves b p = [(pos, neigh) |
pos <- playerCells b p,
neigh <- neighbours (size b) pos,
canAttack b pos neigh]Trying it all out:
ghci> :l DiceOfDoom-c.hs
ghci> attackMoves test2x2Board (Player 0)
[(2,3)]
ghci> attackMoves test2x2Board (Player 1)
[]
ghci> attackMoves test3x3Board (Player 0)
[(8,4)]
ghci> attackMoves test3x3Board (Player 1)
[(1,0),(1,2),(1,5),(4,7),(4,0),(4,5)]Code in DiceOfDoom-c.hs.
Attacking
When an attack is made, the state of the board changes, so we’ll need to write a function that returns this new state.
The Lisp code for this is board-attack. It constructs a new board from the old board
looping through the cells and seeing if one is being attacked or is the attacker. The
Haskell version is similar:
attack :: Board -> Player -> Int -> Int -> Board
attack board p src dest
| canAttack board src dest =
board {
cells = [afterAttack (pos, c) | (pos, c) <- cellPositions board]
}
| otherwise = board
where
srcDice = dice (cells board!! src)
afterAttack (pos, cell)
-- Attacker cell is just left with 1 die
| pos == src = cell { dice = 1}
-- Defender cell switches players and gets remaining dice
| pos == dest = cell { dice = srcDice - 1, player = p}
-- Not involved in the attack
| otherwise = cell Reinforcements
After a player’s completed turn, which might include several attacks, reinforcements are added by dividing the conquered dice among the player’s cells, starting from the top and moving from left to right.
Note: The Lisp function is add-new-dice - this is the tail-call optimised one introduced
later in Chapter 15.
Just like the Lisp function, we use a local function to recurse through the board cells:
reinforce :: Board -> Player -> Board
reinforce board p = board {
cells = distributeDice (cells board) (conqueredDice board - 1),
conqueredDice = 0
}
where
distributeDice :: [Cell] -> Int -> [Cell]
distributeDice [] _ = [] -- No cells remaining
distributeDice cs 0 = cs -- No dice remaining
distributeDice (c:cs) remainingDice =
if player c == p && dice c < maxDice board then
-- Give this cell an extra dice
c {dice = dice c + 1} : distributeDice cs (remainingDice -1)
else
-- Continue on
c : distributeDice cs remainingDicePassing Moves vs Attack Moves
One of the rules of the game is that a player cannot pass on their very first move - they must make an attack if they can. After their first move they player has the option of passing or attacking again.
The Lisp code uses NIL as a pass value. We don’t really have an equivalent
in Haskell. Instead, we introduce a new data type for all moves:
data Move = Attack Int Int |
Pass
deriving (Show)We can re-write the code using the new data type:
(Code in DiceOfDoom-d.hs).
-- List all possible attack moves for a given player on a board
attackMoves :: Board -> Player -> [Move]
attackMoves b p = [Attack pos neigh |
(pos, _) <- playerPositions b p,
neigh <- neighbours (size b) pos,
canAttack b pos neigh]
-- Make a move and return the new board
makeAMove :: Board -> Player -> Move -> Board
makeAMove board _ Pass = board
makeAMove board p (Attack src dest)
| canAttack board src dest =
board {
cells = [afterAttack (pos, c) | (pos, c) <- cellPositions board],
conqueredDice = destDice
}
| otherwise =
board
where
srcDice = dice (cells board!! src)
destDice = dice (cells board!! dest)
afterAttack (pos, cell)
-- Attacker cell is just left with 1 die
| pos == src = cell { dice = 1}
-- Defender cell switches players and gets remaining dice
| pos == dest = cell { dice = srcDice - 1, player = p}
-- Not involved in the attack
| otherwise = cell Here it makes sense to rename the attack function to makeAMove. A passing move just returns
the same board.
When a player passes, the next player takes their turn. Remember, there could be any number of players playing, not just A or B.
nextPlayer :: Board -> Player -> Player
nextPlayer board (Player n) = Player ((n + 1) `mod` (numPlayers board))Putting It All Together - The Game Tree
The Lisp code uses an ordinary list to represent the game tree. In Haskell, we
can use the Date.Tree type, where the nodes in the tree reprsent
the game state:
import Data.Tree
data GameState = GameState {
currentPlayer :: Player,
moveMade :: Move,
currentBoard :: Board
}
deriving (Show)
-- The initial tree with the starting position of the game
sampleGameTree :: Tree GameState
sampleGameTree = Node GameState {
currentPlayer = Player 0,
moveMade = Pass,
currentBoard = test2x2Board
} []The first part is the root of the tree. The second part, the empty list, is the sub-tree.
In GHCI, this displays as:
ghci> :t sampleGameTree
sampleGameTree :: Tree GameState
ghci> sampleGameTree
Node {
rootLabel = GameState {
currentPlayer = a,
moveMade = Pass,
currentBoard = Board {
size = 2,
maxDice = 3,
numPlayers = 2,
cells = [b-2,b-2,a-2,b-1]
}
},
subForest = []
}The next move is A attacking from 2 to 3. This is added to the tree:
sampleGameTreeNext :: Tree GameState
sampleGameTreeNext = Node GameState {
currentPlayer = Player 0,
moveMade = Pass,
currentBoard = test2x2Board
} [Node GameState {
currentPlayer = Player 0,
moveMade = Attack 2 3,
currentBoard = makeAMove test2x2Board (Player 0) (Attack 2 3)
} [] ]In GHCI:
ghci> sampleNextGameTree
Node {
rootLabel = GameState {
currentPlayer = a,
moveMade = Pass,
currentBoard = Board {
size = 2,
maxDice = 3,
numPlayers = 2,
cells = [b-2,b-2,a-2,b-1]
}
},
subForest = [
Node {
rootLabel = GameState {
currentPlayer = a,
moveMade = Attack 2 3,
currentBoard = Board {
size = 2,
maxDice = 3,
numPlayers = 2,
cells = [b-2,b-2,a-1,a-1]
}
},
subForest = []}]}To produce the game tree we get the current root node, find all possible moves (including a ‘Pass’ move if it isn’t the player’s first turn) and for each one of these moves, re-generate the board. The ‘Pass’ move will switch players, adding reinforcements if available. We also switch if there are no moves possible. We recursively do this until we’ve exhausted all possible moves. If we can’t make a move on our first turn, the game ends.
Note that the Haskell version here is a bit different in structure from the Lisp version. The
logic is the same, but I personally don’t like functions that recursively call other
functions - I prefer to keep everything in one. This is why the attackMoves function
doesn’t generate part of the game tree - it just calculates the attacking moves.
gameTree :: Board -> Player -> Move -> Bool -> Tree GameState
gameTree board p fromMove isFirstMove
-- Deliberate Pass
| fromMove == Pass && not isFirstMove =
gameTree
(reinforce board p) -- Add reinforcements
(nextPlayer board p) -- Switch player
Pass -- Passing move
True -- First move for new player
-- No further moves possible. Switch players and add the reinforcements
| null possibleMoves && not isFirstMove =
Node GameState {
currentPlayer = p,
moveMade = fromMove,
currentBoard = board
} [gameTree
(reinforce board p) -- Add reinforcements
(nextPlayer board p) -- Switch player
Pass -- Passing move
True] -- First move for new player
-- Keeping with the same player, recurse through all moves
| otherwise =
Node GameState {
currentPlayer = p,
moveMade = fromMove,
currentBoard = board
} [gameTree (makeAMove board p m) p m False
| m <- possibleMoves ++ addPassingMove]
where
possibleMoves = attackMoves board p
addPassingMove = if isFirstMove
then []
else [Pass]We can test it out. First, if player B starts off on the 2x2 board, there are no further moves possible:
ghci> :l DiceOfDoom-d.hs
ghci> gameTree test2x2Board (Player 1) Pass 0 True
Node {
rootLabel = GameState {
currentPlayer = b,
moveMade = Pass,
currentBoard = [b-2,b-2,a-2,b-1], reinforcements : 0
},
subForest = []}The Board’s Show instance has been implemented to just show cells and conquered dice:
instance Show Board where
show b = show (cells b) ++ ", reinforcements : " ++ show (conqueredDice b)Next, if player A starts off, we get a fuller game tree:
ghci> gameTree test2x2Board (Player 0) Pass 0 True
Node{
rootLabel=GameState{ currentPlayer=a, moveMade=Pass, currentBoard=[ b-2, b-2, a-2, b-1 ], reinforcements: 0 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=a, moveMade=Attack 2 3, currentBoard=[ b-2, b-2, a-1, a-1 ], reinforcements: 1 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=b, moveMade=Pass, currentBoard=[ b-2, b-2, a-1, a-1 ], reinforcements: 0 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=b, moveMade=Attack 0 2, currentBoard=[ b-1, b-2, b-1, a-1 ], reinforcements: 1 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=b, moveMade=Attack 1 3, currentBoard=[ b-1, b-1, b-1, b-1 ], reinforcements: 1 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=a, moveMade=Pass, currentBoard=[ b-1, b-1, b-1, b-1 ], reinforcements: 0 },
subForest=[ ] } ] } ]
},
Node{
rootLabel=GameState{ currentPlayer=b, moveMade=Attack 0 3, currentBoard=[ b-1, b-2, a-1, b-1 ], reinforcements: 1 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=a, moveMade=Pass, currentBoard=[ b-1, b-2, a-1, b-1 ], reinforcements: 0 },
subForest=[ ] } ]
},
Node{
rootLabel=GameState{ currentPlayer=b, moveMade=Attack 1 3, currentBoard=[ b-2, b-1, a-1, b-1 ], reinforcements: 1 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=b, moveMade=Attack 0 2, currentBoard=[ b-1, b-1, b-1, b-1 ], reinforcements: 1 },
subForest=[
Node{
rootLabel=GameState{ currentPlayer=a, moveMade=Pass, currentBoard=[ b-1, b-1, b-1, b-1 ], reinforcements: 0 },
subForest=[ ] } ] } ] } ] } ] } ] }Code in DiceOfDoom-d.hs
Playing - Human vs Human
We’ve got all the pieces now to allow a human play against another human.
Given a node in a game tree, we
- Print the current game state
- If there are no child nodes then the game has ended - announce the winner.
- If there are child nodes, print out the possible moves, let the player make that move and recurse.
playVsHuman :: Tree GameState -> IO ()
playVsHuman (Node root children) = do
printGameState (Node root children)
if not (null children)
then
playVsHuman =<< handleHuman tree
else
announceWinner $ currentBoard root
printGameState :: Tree GameState -> IO ()
printGameState (Node root _) = do
putStrLn $ "Current player: " ++ show (currentPlayer root)
drawBoard $ currentBoard rootThere can be more than one winner in a game - a draw is possible in a 2-player game and a draw is possible between 2 or more players in a N-player game.
announceWinner :: Board -> IO ()
announceWinner board =
putStrLn $
if length whoWon > 1
then "The result is a tie between " ++ unwords (map show whoWon)
else "The winner is " ++ show (head whoWon)
where
whoWon = winners board
winners :: Board -> [Player]
winners board = [head p | p <- players, length p == length (head players)]
where
players = sortBy (flip compare `on` length)
$ group
$ sort [player c | c <- cells board]Handling the human input is another ‘dirty’ function. Given a game tree, tell the human what their options are and ask for input, returning the subtree that they chose:
handleHuman :: Tree GameState -> IO (Tree GameState)
handleHuman tree@(Node _ children) = do
putStrLn "choose your move:"
putStr $ showChoice allowedMoves
userInput <- getLine
let choice = read userInput :: Int
case Map.lookup choice mapOfMoves of
Just _ ->
return $ children !! (choice - 1)
Nothing -> do
putStrLn "Invalid choice. Choose again."
handleHuman tree
where
allowedMoves :: [(Int, Move)]
allowedMoves = zip [1..] [moveMade c | (Node c _) <- children]
showChoice :: [(Int, Move)] -> String
showChoice choices = unlines [show num ++ ": " ++ show move | (num, move) <- choices]
mapOfMoves :: Map.Map Int Move
mapOfMoves = Map.fromList allowedMovesThe code uses Data.Map to create a map between choices numbers and the child nodes in the tree.
Let’s give it a shot:
ghci> :l DiceOfDoom-e.hs
ghci> playVsHuman $ gameTree test2x2Board (Player 0) Pass True
Current player: a
b-2 b-2
a-2 b-1
choose your move:
1: Attack 2 3
1
Current player: a
b-2 b-2
a-1 a-1
choose your move:
1: Pass
1
Current player: b
b-2 b-2
a-1 a-1
choose your move:
1: Attack 0 2
2: Attack 0 3
3: Attack 1 3
1
Current player: b
b-1 b-2
b-1 a-1
choose your move:
1: Attack 1 3
2: Pass
1
Current player: b
b-1 b-1
b-1 b-1
choose your move:
1: Pass
1
Current player: a
b-1 b-1
b-1 b-1
The winner is bThat’s it for part 1. In the next part we’ll work on the AI player, and start worrying about performance and optimisation.